![]() On appelle univers, et on note
On appelle univers, et on note ![]() , l’ensemble des issues liées à une expérience aléatoire.
, l’ensemble des issues liées à une expérience aléatoire.
On considère l’ensemble ![]() , appelé tribu, des parties de
, appelé tribu, des parties de ![]() obtenues par unions finies ou dénombrables d’éléments de
obtenues par unions finies ou dénombrables d’éléments de ![]() ainsi que par passage au complémentaire. Les éléments de
ainsi que par passage au complémentaire. Les éléments de ![]() seront appelés évènements.
seront appelés évènements.
![]() On appelle mesure sur
On appelle mesure sur ![]() toute fonction
toute fonction ![]() :
:
![]() Positive:
Positive: ![]() ,
, ![]()
![]() Additive:
Additive: ![]() implique
implique ![]()
Si ![]() , on dit que
, on dit que ![]() est une probabilité sur
est une probabilité sur ![]() que nous noterons désormais
que nous noterons désormais ![]()
![]()
![]() tel que
tel que ![]() on appelle probabilité conditionnelle, et on note
on appelle probabilité conditionnelle, et on note ![]() , la probabilité définie sur
, la probabilité définie sur ![]() par
par
![]()
![]()
On retiendra : ![]() )
)
Si ![]() est une partition de
est une partition de ![]() , (
, (![]() et
et ![]() ), on a alors pour tout évènement
), on a alors pour tout évènement ![]() :
:
![]()
![]() On appelle variable aléatoire toute application
On appelle variable aléatoire toute application ![]() d’un espace probabilisé
d’un espace probabilisé ![]() dans
dans ![]() et on appelle loi de X la mesure
et on appelle loi de X la mesure ![]() définie sur
définie sur ![]() par :
par : ![]() , que l’on note généralement
, que l’on note généralement ![]()
Exemple1 ( cas discret)
On lance deux dés, soit ![]() le maximum obtenu.
le maximum obtenu. ![]() prend les valeurs 1 ,2, 3, 4, 5 ou 6.
prend les valeurs 1 ,2, 3, 4, 5 ou 6.
Loi de ![]() :
:
![]() ( seule l’issue
( seule l’issue![]() correspond à un maximum de 1)
correspond à un maximum de 1)
![]()
![]()
…
![]()
![]() On dit que
On dit que ![]() a une densité
a une densité ![]() si pour tout
si pour tout ![]() :
:
![]()
![]() est la fonction indicatrice de
est la fonction indicatrice de ![]() , elle vaut 1 sur
, elle vaut 1 sur ![]() et 0 ailleurs.
et 0 ailleurs.
Exemple2 (cas continu)
Supposons que ![]() a pour densité la fonction
a pour densité la fonction ![]() sur
sur ![]()
Premièrement, on doit avoir ![]() donc
donc ![]()
![]() , donc
, donc ![]()
Deuxièmement, calculons ![]()
![]()
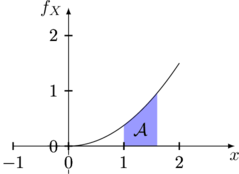
L’aire hachurée ci-dessus « mesure » le segment ![]() .
.
![]() Deux événements sont indépendants si et seulement si
Deux événements sont indépendants si et seulement si ![]() .
.
![]() On appelle fonction de répartition la fonction définie sur
On appelle fonction de répartition la fonction définie sur ![]() par
par ![]()
Dans le cas discret, ![]() , par exemple avec l’exemple 1:
, par exemple avec l’exemple 1:
![]()
Dans le cas continu,![]() et on a alors :
et on a alors :
![]() ( TRES pratique, voir exemple suivant )
( TRES pratique, voir exemple suivant )
![]() Si on dispose de 2 variables aléatoires, il est alors possible de définir la loi du couple
Si on dispose de 2 variables aléatoires, il est alors possible de définir la loi du couple ![]() par
par
![]()
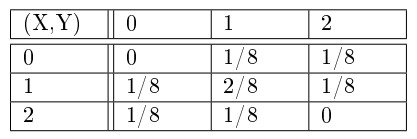
Exemple 3 :
On lance trois fois une pièce équilibrée on note X le nombre de « face » obtenus aux deux premiers lancers et Y le nombre de « pile » obtenus aux deux derniers lancers. La loi du couple est donnée dans le tableau ci-dessous:
Exemple de calcul:
pour ![]()
![]() La loi du couple
La loi du couple![]() permet de retrouver les lois dites marginales de
permet de retrouver les lois dites marginales de ![]() et de
et de ![]() ( l’inverse n’est pas vrai ) , en effet :
( l’inverse n’est pas vrai ) , en effet :
![]() Avec l’exemple précédent,
Avec l’exemple précédent, ![]()
![]() Si 2 variables aléatoires sont indépendantes:
Si 2 variables aléatoires sont indépendantes: ![]()
Exemple 4
Si ![]() et
et ![]() de loi
de loi ![]() , (
, (![]() ), indépendantes alors:
), indépendantes alors:
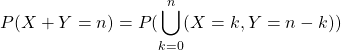
![]() (car évènements disjoints)
(car évènements disjoints)
![]() (car
(car ![]() indépendantes )
indépendantes )
![]()
![]()
Exemple 5
![]() et
et ![]() sont deux variables aléatoires indépendantes qui suivent toutes les deux une loi exponentielle de paramètre 1 ( voir section suivante) , déterminer la loi de
sont deux variables aléatoires indépendantes qui suivent toutes les deux une loi exponentielle de paramètre 1 ( voir section suivante) , déterminer la loi de ![]() . On utilise ici la fonction de répartition.
. On utilise ici la fonction de répartition.
![]() , par indépendance.
, par indépendance.
![]()
Puis on dérive cette expression pour obtenir la densité de ![]() :
: ![]()
![]() Un petit point théorique:
Un petit point théorique:
On considère ici un espace de probabilité ![]() , et une variable aléatoire
, et une variable aléatoire ![]() définie sur
définie sur ![]() , de loi de probabilité
, de loi de probabilité ![]() .
.
Théorème de transfert : Soit ![]() une fonction mesurable réelle définie sur
une fonction mesurable réelle définie sur ![]() .
. ![]() est P-intégrable si et seulement si
est P-intégrable si et seulement si ![]() est
est ![]() -intégrable, et l’on a :
-intégrable, et l’on a :
![]()
![]() On appelle espérance de la variable aléatoire
On appelle espérance de la variable aléatoire ![]() le nombre:
le nombre:
![]() … ce qui grâce au théorème de transfert donne :
… ce qui grâce au théorème de transfert donne :
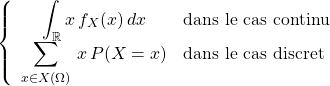
Remarques:
1) Soit ![]() une fonction mesurable réelle définie sur
une fonction mesurable réelle définie sur ![]() . Alors
. Alors ![]() est aussi une v.a.r. définie sur l’espace de probabilité
est aussi une v.a.r. définie sur l’espace de probabilité ![]() . Par conséquent, si elle est P-intégrable, elle possède une espérance, qui d’après le théorème de transfert, est égale à:
. Par conséquent, si elle est P-intégrable, elle possède une espérance, qui d’après le théorème de transfert, est égale à:
![]()
![]() si
si ![]() a pour densité
a pour densité ![]()
… et il est donc possible de calculer ![]() sans connaitre la loi de
sans connaitre la loi de ![]() !
!
2)La loi d’une variable aléatoire X à valeurs dans ![]() est uniquement déterminée par le calcul de
est uniquement déterminée par le calcul de ![]() pour toute fonction
pour toute fonction ![]() réelle continue positive bornée. Autrement dit si il existe
réelle continue positive bornée. Autrement dit si il existe ![]() telle que :
telle que :
![]() alors
alors ![]() est la densité de
est la densité de ![]() .
.
Exemple 6:
Si ![]() a pour densité
a pour densité ![]() sur
sur ![]() , déterminer la loi de
, déterminer la loi de ![]() .
.
![]()
![]()
![]() changement de variable
changement de variable ![]()
![]()
donc la loi de ![]() est
est ![]() (Loi exponentielle de paramètre
(Loi exponentielle de paramètre ![]() )
)
![]() Exemples de calcul d’espérance:
Exemples de calcul d’espérance:
a) Pour une loi binomiale: ![]() ,
, ![]()
![]()
![]()
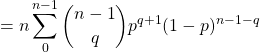
![]()
![]() Attention au changement d’indice :
Attention au changement d’indice :![]()
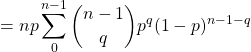
![]() Rappel :
Rappel :![]()
b) Pour une loi exponentielle : ![]()
![]()
![]()
![]() On appelle variance de la variable aléatoire
On appelle variance de la variable aléatoire ![]() le nombre:
le nombre:
![]()
![]() ( Deuxième formule souvent plus pratique).
( Deuxième formule souvent plus pratique).
![]() Propriétés
Propriétés
![]()
![]()
Si ![]() sont des variable aléatoire indépendantes alors:
sont des variable aléatoire indépendantes alors:
![]() et
et ![]()
![]() Deux inégalités faisant intervenir l’espérance et la variance:
Deux inégalités faisant intervenir l’espérance et la variance:
a) Inégalité de Markov : Si ![]() est définie sur
est définie sur ![]() , pour tout réel
, pour tout réel ![]() > 0,
> 0,
![]()
En effet ![]()
![]()
donc ![]()
et donc ![]()
b) Inégalité de Bienaymé-Chebychev : Si ![]() , alors pour tout réel
, alors pour tout réel ![]() ,
,
![]()
Il suffit d’appliquer l’inégalité de Markov à la variable aléatoire ![]() .
.
Exemple 7 :
Un dé est lancé 9 000 fois. Déterminer un minorant de la probabilité de l’événement ”On a obtenu ”6” entre1400 et 1600 fois”.
Notons X le nombre de fois où on a obtenu ”6” au cours de ces 9 000 lancers. On cherche un minorant pour ![]() .
.
On sait que X suit une loi binomiale ![]() , d’espérance 1500 et de variance 1250.
, d’espérance 1500 et de variance 1250.
Comme ![]() ,
, ![]()
Soit ![]() , et avec
, et avec ![]() :
:
![]()
En comparant avec la valeur exacte, on constate que cette minoration est assez grossière .
Remarque : En utilisant l’inégalité de Bienaymé-Tchebychev, on peut déduire que si X est une variable aléatoire de carré intégrable et non constante alors plus de 88![]() des valeurs observées de
des valeurs observées de ![]() se trouvent dans l’intervalle
se trouvent dans l’intervalle ![]() .
.
Plus généralement, pour tout ![]() ,
, ![]()
Rappel : ![]() est la racine carrée de la variance, appelé écart-type.
est la racine carrée de la variance, appelé écart-type.
![]() On définit la covariance de deux variables aléatoires réelles
On définit la covariance de deux variables aléatoires réelles ![]() par la formule:
par la formule:
![]()
Deux variables aléatoires ![]() sont dites non corrélées si leur covariance est nulle (Par exemple si
sont dites non corrélées si leur covariance est nulle (Par exemple si ![]() indépendantes
indépendantes ![]() sont dites non corrélées.) sinon on appelle coefficient de corrélation du couple
sont dites non corrélées.) sinon on appelle coefficient de corrélation du couple ![]() le nombre :
le nombre :
![]()
On a ![]() .
.
Et si ![]() alors
alors ![]() et
et ![]() sont liées par une relation affine.
sont liées par une relation affine.
![]() On généralise la notion de couple de variables aléatoires à la dimension
On généralise la notion de couple de variables aléatoires à la dimension ![]() , on parle alors du « vecteur aléatoire »
, on parle alors du « vecteur aléatoire » ![]() ou plus précisément de variable aléatoire à valeurs dans
ou plus précisément de variable aléatoire à valeurs dans ![]() .
.
Alors ![]() et
et
Les lois classiques
Lois discrètes
a) Loi uniforme. Soit ![]() ensemble fini de cardinal
ensemble fini de cardinal ![]() ,
, ![]() est une variable uniforme sur
est une variable uniforme sur ![]() si
si ![]() .
.
![]()
b) Loi de Bernoulli de paramètre ![]() , notée
, notée ![]() : X à valeurs dans
: X à valeurs dans ![]() telle que
telle que ![]() .
.
![]()
c) Loi binomiale de paramètres ![]()
![]() , notée
, notée ![]() est la loi de la somme de
est la loi de la somme de ![]() variables indépendantes identiquement distribuées de Bernoulli de paramètre
variables indépendantes identiquement distribuées de Bernoulli de paramètre ![]() . X prend ses valeurs dans
. X prend ses valeurs dans ![]() et:
et:
![]() .
.
![]()
d) Loi géométrique de paramètre ![]() , notée
, notée ![]() : X à valeurs dans
: X à valeurs dans ![]() telle que
telle que ![]() .
.
![]()
e) Loi de Poisson de paramètre ![]() , notée
, notée ![]() : X à valeurs dans N telle que
: X à valeurs dans N telle que ![]() .
.
![]()
Lois continues
a) Loi uniforme sur ![]() (a < b), notée
(a < b), notée ![]() : de densité
: de densité ![]() .
.
![]()
b) Loi exponentielle de paramètre ![]() , notée
, notée ![]() : de densité
: de densité ![]() .
.
![]()
c) Loi gaussienne (ou normale) de moyenne ![]() et de variance
et de variance ![]() , notée
, notée ![]() : de densité
: de densité ![]()
Quelques remarques importantes :
![]() Les lois géométriques et exponentielles ont en commun la propriété dite de « non vieillissement « :
Les lois géométriques et exponentielles ont en commun la propriété dite de « non vieillissement « :
![]()
Exemple de calcul pour la loi exponentielle:
![]()
… et comme pour cette loi, ![]() ,
, ![]() , donc:
, donc:
![]()
![]() Si
Si ![]() suit une loi
suit une loi ![]() , alors
, alors ![]() suit une loi
suit une loi ![]() et les calculs s’effectuent à l’aide de la fonction de répartition de celle-ci fournie en annexe.
et les calculs s’effectuent à l’aide de la fonction de répartition de celle-ci fournie en annexe.
Exemple 8
![]() suit une loi
suit une loi ![]() (Attention 4=
(Attention 4=![]() ), calculer
), calculer ![]() .
.
![]() suit une loi
suit une loi ![]() et
et ![]() =
=![]()
![]()
![]() se lit directement dans la table, à l’intersection de la ligne
se lit directement dans la table, à l’intersection de la ligne ![]() et de la colonne
et de la colonne ![]() , soit :
, soit : ![]()
Pour ![]() on utilise la symétrie de la courbe de densité:
on utilise la symétrie de la courbe de densité:
![]()
Et finalement ![]()
Premières notions de statistiques
Un test d’hypothèse est un procédé d’inférence ( inférer signifie tirer une conclusion ou une conséquence à partir d’un fait ) permettant d’accepter ou rejeter, à partir de l’étude d’un ou plusieurs échantillons aléatoires, la validité d’hypothèses relatives à une ou plusieurs populations.
Les méthodes de l’inférence statistique nous permettent de déterminer, avec une probabilité donnée, si les différences constatées au niveau des échantillons peuvent être imputables au hasard ou si elles sont suffisamment importantes pour signifier que les échantillons proviennent de populations vraisemblablement différentes.
Le principe des tests d’hypothèse est de poser une hypothèse de travail et de prédire les conséquences de cette hypothèse pour la population ou l’échantillon. On compare ces prédictions avec les observations et l’on conclut en acceptant ou en rejetant l’hypothèse de travail à partir de règles de décisions objectives.
Différentes étapes doivent être suivies pour tester une hypothèse :
(1) définir l’hypothèse nulle, notée ![]() , à contrôler ;
, à contrôler ;
(2) choisir une statistique ( Voir plus bas) pour contrôler ![]() ;
;
(3) définir la distribution de la statistique sous l’hypothèse « ![]() est réalisée » ;
est réalisée » ;
(4) définir le niveau de signification du test ![]() et la région critique associée ;
et la région critique associée ;
(5) calculer, à partir des données fournies par l’échantillon, la valeur de la statistique ;
(6) prendre une décision concernant l’hypothèse posée .
L’hypothèse nulle notée ![]() est l’hypothèse que l’on désire contrôler : elle consiste à dire qu’il n’existe pas de différence entre les paramètres comparés ou que la différence observée n’est pas significative et est due aux fluctuations d’échantillonnage. Cette hypothèse est formulée dans le but d’être rejetée.
est l’hypothèse que l’on désire contrôler : elle consiste à dire qu’il n’existe pas de différence entre les paramètres comparés ou que la différence observée n’est pas significative et est due aux fluctuations d’échantillonnage. Cette hypothèse est formulée dans le but d’être rejetée.
Une statistique est une fonction des variables aléatoires représentant l’échantillon.
Connaissant la loi de probabilité suivie par la statistique ![]() sous l’hypothèse
sous l’hypothèse ![]() , il est possible d’établir une valeur seuil,
, il est possible d’établir une valeur seuil, ![]() de la statistique pour une probabilité donnée appelée le niveau de signification
de la statistique pour une probabilité donnée appelée le niveau de signification ![]() du test.
du test.
La région critique ![]() correspond à l’ensemble des valeurs telles que :
correspond à l’ensemble des valeurs telles que : ![]() .
.
Sous l’hypothèse « ![]() est vraie » et pour un seuil de signification
est vraie » et pour un seuil de signification ![]() fixé:
fixé:
– si la valeur de la statistique ![]() calculée appartient à la région critique alors l’hypothèse
calculée appartient à la région critique alors l’hypothèse ![]() est rejetée au risque d’erreur
est rejetée au risque d’erreur ![]() et l’hypothèse alternative
et l’hypothèse alternative ![]() est acceptée .
est acceptée .
Rejet erroné de ![]() : On appelle risque d’erreur de première espèce la probabilité de rejeter
: On appelle risque d’erreur de première espèce la probabilité de rejeter ![]() (et d’accepter
(et d’accepter ![]() !) alors que
!) alors que ![]() est vraie .
est vraie .
Choix erroné de ![]() : On appelle risque d’erreur de seconde espèce, notée
: On appelle risque d’erreur de seconde espèce, notée ![]() la probabilité de rejeter
la probabilité de rejeter ![]() (et d’accepter
(et d’accepter ![]() ) alors que
) alors que ![]() est vraie .
est vraie .
Rejeter ![]() avec raison: On appelle \textit{puissance} d’un test, la probabilité de rejeter
avec raison: On appelle \textit{puissance} d’un test, la probabilité de rejeter ![]() et d’accepter
et d’accepter ![]() alors que
alors que ![]() est vraie. Sa valeur est
est vraie. Sa valeur est ![]()
Exemple 9
On s’intéresse à la probabilité ![]() d’observer un certain phénotype sur un individu issu d’un croisement. Selon que le phénotype est déterminé par un gène ou par 2 gènes situés sur des chromosomes différents, la probabilité p d’observer ce phénotype sera
d’observer un certain phénotype sur un individu issu d’un croisement. Selon que le phénotype est déterminé par un gène ou par 2 gènes situés sur des chromosomes différents, la probabilité p d’observer ce phénotype sera ![]() ou
ou ![]() .
.
On réalise 50 croisements indépendants, et on note X le nombre d’individus présentant le phénotype.
Notons ![]() « contre »
« contre » ![]()
On considère le rapport des vraisemblances: ![]()
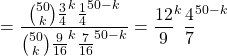
Pour quelle valeur de ![]() a-t-on
a-t-on ![]() ?
?
![]() si
si ![]() soit
soit ![]()
Soit 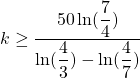 c’est à dire 34.
c’est à dire 34.
La règle de décision sera donc la suivante : On accepte ![]() si le nombre de réalisations de
si le nombre de réalisations de ![]() est supérieur à 34.
est supérieur à 34.
le niveau de ce test est alors ![]()
La puissance de ce test est alors ![]()
D’autres lois fondamentales pour les statistiques
![]() La loi multinomiale :
La loi multinomiale :
On répète ![]() fois une expérience à
fois une expérience à ![]() issues de probabilités respectives
issues de probabilités respectives ![]() de façon indépendante et on note
de façon indépendante et on note ![]() le nombre de réalisations de l’issue
le nombre de réalisations de l’issue ![]() .
.
Le vecteur aléatoire ![]() suit une loi multinomiale de paramètres
suit une loi multinomiale de paramètres ![]() et on a :
et on a :
![]()
Chaque ![]() suit une loi binomiale de paramètres
suit une loi binomiale de paramètres ![]() .
.
![]()
Exemple 9(bis):
Une expérience comporte 3 issues de probabilités respectives ![]() , calculer
, calculer ![]() si on réalise 4 fois cette expérience.
si on réalise 4 fois cette expérience.
![]()
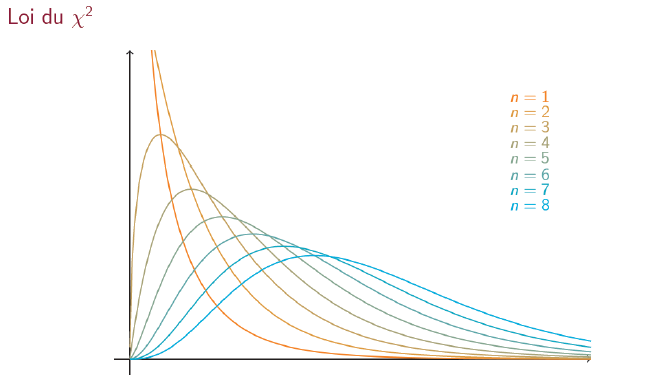
![]() Loi du khi-deux
Loi du khi-deux ![]() :
:
Si ![]() suit une loi du khi-deux à
suit une loi du khi-deux à ![]() degrés de liberté alors la densité de
degrés de liberté alors la densité de ![]() est alors:
est alors: ![]() , pour
, pour ![]() où
où ![]() est la fonction définie par
est la fonction définie par ![]()
Là encore aucun calcul ne sera effectuer directement , on utilisera systématiquement les tables (voir annexe), mais attention la présentation des tables n’est pas la même d’une loi à l’autre.
![]() et
et ![]()
Allure des fonctions densité :
Résultat fondamental : Si ![]() sont des variable aléatoires indépendantes qui suivent la loi normale
sont des variable aléatoires indépendantes qui suivent la loi normale ![]() alors
alors ![]() suit une loi du khi-deux à
suit une loi du khi-deux à ![]() degrés de liberté. ( Voir la Démonstration en annexe).
degrés de liberté. ( Voir la Démonstration en annexe).
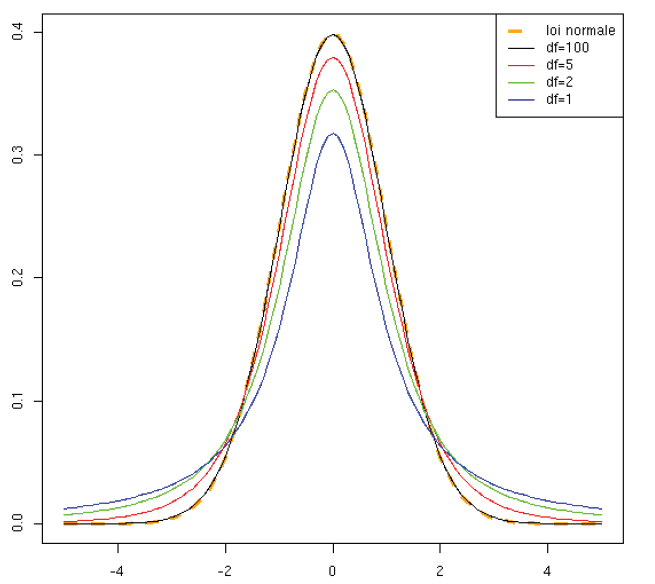
![]() Loi de Student
Loi de Student ![]() :
:
Si ![]() suit une
suit une ![]() et
et ![]() suit une
suit une ![]() , alors la variable aléatoire
, alors la variable aléatoire 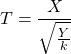 suit une loi de Student à
suit une loi de Student à![]() degrés de liberté.
degrés de liberté.
La densité de ![]() est alors:
est alors: ![]()
![]() et
et ![]()
Allure de la fonction densité :
Fonctions caractéristiques
Un outil indispensable pour la suite, il s’agit de la fonction caractéristique d’une variable aléatoire ![]() :
:
![]() (attention on utilise ici les nombres complexes )
(attention on utilise ici les nombres complexes )
Exemples de calculs
Si ![]() suit une loi de Poisson,
suit une loi de Poisson, ![]() ,
,
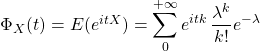
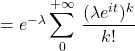
![]()
![]() …
… ![]() (on utilise ici
(on utilise ici 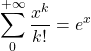 )
)
![]()
![]() Principales propriétés:
Principales propriétés:
1)La fonction caractéristique d’une variable aléatoire caractérise sa loi.
2)![]()
3)Si X et Y sont des variables aléatoires indépendantes, alors pour tout réel t, ![]()
4)Lorsque ![]() ,
,![]()
Si X et Y sont des variables aléatoires indépendantes suivant des lois de poisson de paramètres ![]() et
et ![]() ,
,
![]() … d’après 3)
… d’après 3)
![]()
…. et donc ![]() suit une loi de poisson de paramètre
suit une loi de poisson de paramètre ![]() … d’après 1)
… d’après 1)
Si ![]() suit une loi
suit une loi ![]() ,
,
![]() donc si
donc si ![]() suit une loi
suit une loi ![]() ,
, ![]() … d’après 2)
… d’après 2)
Si X et Y sont des variables aléatoires indépendantes suivant des lois ![]() et
et ![]() alors :
alors :
![]() … d’après 3)
… d’après 3)
![]()
qui est la fonction caractéristique d’une ![]()
![]() Un calcul fondamental :
Un calcul fondamental :
Soit ![]() une suite de variables aléatoires deux à deux indépendantes de même loi
une suite de variables aléatoires deux à deux indépendantes de même loi ![]() , on suppose
, on suppose ![]() et
et ![]() , on note
, on note ![]() la fonction caractéristique de
la fonction caractéristique de ![]() .
.
Soit ![]()
![]()
or d’après 4), ![]()
![]() et comme
et comme ![]() :
:
![]()
![]() (Rappel
(Rappel ![]() en 0)
en 0)
Finalement ![]() qui est la fonction caractéristique d’une loi
qui est la fonction caractéristique d’une loi ![]() , ce qui démontrera le théorème central limite.
, ce qui démontrera le théorème central limite.
Convergence de variables aléatoires
Les différents types de convergence:
Convergence presque sûre : On dit que ![]() converge presque sûrement vers
converge presque sûrement vers ![]() et on note
et on note ![]() si :
si :
![]() sur un ensemble de probabilité 1…d’où l’expression presque sûre
sur un ensemble de probabilité 1…d’où l’expression presque sûre
Convergence en probabilité: On dit que ![]() converge en probabilité vers X et on note
converge en probabilité vers X et on note ![]() si
si
![]()
Convergence en loi : On dit que ![]() converge en loi vers
converge en loi vers ![]() et on note
et on note ![]() si :
si :
![]()
![]() …..(F est la fonction de répartition !)
…..(F est la fonction de répartition !)
ou ![]()
ou, formulation équivalente:
![]() si
si ![]() , une fonction continue ,bornée et positive :
, une fonction continue ,bornée et positive :![]()
Théorème :
![]() converge en loi vers
converge en loi vers ![]() si et seulement si pour
si et seulement si pour
tout ![]() ,
, ![]()
![]() Un exemple important :
Un exemple important :
On a vu que si ![]() suit une loi de Poisson,
suit une loi de Poisson, ![]()
Pour une loi de Bernoulli, ![]()
Donc pour une loi Binomiale ![]() où les
où les ![]() sont des variables de Bernoulli:
sont des variables de Bernoulli:
![]()
donc si ![]() suit une loi binomiale de paramètres
suit une loi binomiale de paramètres ![]() , on a:
, on a:
![]() , donc
, donc ![]()
…qui tend vers ![]() lorsque
lorsque ![]() et donc :
et donc :
![]() qui est la fonction caractéristique de la loi de Poisson , ce qui démontre la convergence en loi d’une loi de Bernoulli vers une loi de Poisson .
qui est la fonction caractéristique de la loi de Poisson , ce qui démontre la convergence en loi d’une loi de Bernoulli vers une loi de Poisson .
Exemple 10:
Dans une chaîne de fabrication, 5![]() des pièces sont défectueuses, on prélève une pièce, on examine si elle est défectueuse et on la replace parmi les autres. On répète 120 fois cette expérience. On désigne par
des pièces sont défectueuses, on prélève une pièce, on examine si elle est défectueuse et on la replace parmi les autres. On répète 120 fois cette expérience. On désigne par ![]() la variable aléatoire qui à chaque tirage de 120 pièces associe le nombre des pièces défectueuses, calculer
la variable aléatoire qui à chaque tirage de 120 pièces associe le nombre des pièces défectueuses, calculer ![]()
![]() suit une
suit une ![]() , avec
, avec ![]() ,
, ![]()
Un autre exemple important de convergence
Rappel :
Si ![]() suivent une loi de loi de Bernoulli de même paramètre
suivent une loi de loi de Bernoulli de même paramètre ![]() , indépendantes, alors
, indépendantes, alors ![]() suit
suit
une loi binomiale de paramètres ![]()
L’inégalité de Chebychev nous donne pour tout ![]() :
:
![]() (
(![]() !)
!)
Et pour une loi binomiale ![]() , donc :
, donc :
![]()
et donc ![]()
ce qui démontre la convergence en probabilité de ![]() vers
vers ![]()
On retiendra les liens entre les différentes notions de convergence par le diagramme suivant.
Convergence presque sûre ![]() Convergence en probabilité
Convergence en probabilité ![]() Convergence en loi
Convergence en loi
Le résultat de l’exemple précédent se généralise à d’autres types de lois, et à des v.a.r. indépendantes deux à deux et non corrélées deux à deux.
Loi faible des grands nombres :
Soient ![]() des variables aléatoires indépendantes et de même loi, si
des variables aléatoires indépendantes et de même loi, si ![]() alors :
alors :
![]()
En effet on note 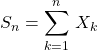 ,
, ![]() et
et ![]() . Alors,
. Alors,
![]()
En particulier, ![]()
On dispose même d’un résultat plus précis :
Loi forte des grands nombres :
Soient ![]() des variables aléatoires indépendantes et de même loi, si
des variables aléatoires indépendantes et de même loi, si ![]() alors :
alors :
![]()
Le théorème central limite:
La loi des grands nombres nous dit qu’en présence d’une suite ![]() de variables aléatoires indépendantes et de même loi, la moyenne empirique
de variables aléatoires indépendantes et de même loi, la moyenne empirique ![]() converge vers la moyenne théorique
converge vers la moyenne théorique ![]() . Cependant, nous ne savons rien des fluctuations autour de cette moyenne théorique.
. Cependant, nous ne savons rien des fluctuations autour de cette moyenne théorique.
Soient ![]() des variables aléatoires indépendantes et de même loi, notons
des variables aléatoires indépendantes et de même loi, notons ![]() et
et ![]() , alors :
, alors :
![]()
(Voir démonstration partie 4)
Exemple 11: On lance un dé non pipé 100 fois, de façon bien entendu indépendante. Quelle est la probabilité que la somme totale des points obtenus soit entre 300 et 400 ?
La somme totale est 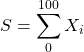 où
où ![]() représente le nombre de points obtenus.
représente le nombre de points obtenus.
L’espérance de ![]() est 3,5 et sa variance est 35/12.
est 3,5 et sa variance est 35/12.
Par le TCL![]() suit approximativement une loi
suit approximativement une loi ![]() donc:
donc:
![]() )
)
![]()
![]() …. d’après le table
…. d’après le table
Ce théorème a son pendant vectoriel.
Soit ![]() une suite de vecteurs aléatoires du second ordre indépendants, de même loi, d’espérance
une suite de vecteurs aléatoires du second ordre indépendants, de même loi, d’espérance ![]() , de matrice de variances-covariances
, de matrice de variances-covariances ![]()
Alors: ![]()
Le gros théorème
![]() Soit
Soit![]() une loi de probabilité sur
une loi de probabilité sur ![]() et
et ![]() un échantillon de loi
un échantillon de loi ![]() .
.
On définit les variables aléatoires ![]() à valeurs dans
à valeurs dans ![]() par
par ![]() .
.
On dit que le vecteur ![]() suit la loi multinomiale de paramètre
suit la loi multinomiale de paramètre ![]() .
.
Lorsque ![]() tend vers l’infini alors la variable
tend vers l’infini alors la variable 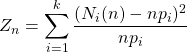 converge en loi vers la loi du
converge en loi vers la loi du ![]() à
à ![]() degrés de liberté.
degrés de liberté.
![]() Dans le cas
Dans le cas ![]() ,
, ![]() ,
, ![]() or
or ![]() et
et ![]() et donc
et donc ![]() et
et
![]()
Rappel : ![]() suit une loi binomiale qui est la somme de
suit une loi binomiale qui est la somme de ![]() variables de Bernoulli d’éspérance
variables de Bernoulli d’éspérance ![]() et de variance
et de variance ![]() donc d’après le T.C.L,
donc d’après le T.C.L, ![]() converge vers une
converge vers une ![]() et donc
et donc ![]() converge vers la loi du
converge vers la loi du ![]() à 1 degré de liberté.
à 1 degré de liberté.
Pour la démonstration, plus difficile, du cas général on remarquera que ![]() est la norme du vecteur de coordonnées
est la norme du vecteur de coordonnées ![]() lequel est orthogonal au vecteur
lequel est orthogonal au vecteur ![]() (faire le calcul avec
(faire le calcul avec 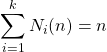 et
et 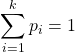 . et la démonstration se termine dans une base orthonormée quelconque de l’hyperplan orthogonal à
. et la démonstration se termine dans une base orthonormée quelconque de l’hyperplan orthogonal à ![]()
Il est alors possible de mettre en place les premiers tests statistiques :
![]() Test d’adéquation à une loi donnée .
Test d’adéquation à une loi donnée .
On dispose d’observations que l’on considère comme des réalisations indépendantes et identiquement distribuées. de loi ![]() inconnue.
inconnue.
On souhaite ici construire un test qui permette de répondre à la question suivante : la loi des observations est-elle ![]() ?
?
En termes statistiques, on souhaite tester l’hypothèse ![]()
![]()
On note ![]() le niveau du test , généralement
le niveau du test , généralement ![]() , ce qui signifie qu’on choisit une région de rejet égale à
, ce qui signifie qu’on choisit une région de rejet égale à ![]() ou
ou ![]() est le quantile d’ordre
est le quantile d’ordre ![]() de la loi
de la loi ![]() . (
. (![]() ).
).
La règle de décision est la suivante. On calcule ![]() grâce aux observations. Si
grâce aux observations. Si ![]() alors on rejette
alors on rejette ![]() , sinon on l’accepte .
, sinon on l’accepte .
Exemple 12
Deux cobayes (génération 0) de lignées pures dont les pelages sont gris et lisse pour le premier et blanc et rude pour le second ont donné une progéniture homogène au pelage gris et lisse. En croisant ces cobayes de la génération 1 entre eux, on a obtenu 64 descendants dont les pelages se répartissent de la manière indiquée dans le tableau suivant :
Faisons les hypothèses de modélisation suivantes (on parle de modèle mendélien) :
– les cobayes sont des animaux diploïdes
– le gène responsable de la couleur du pelage est présent sous la forme de deux allèles, l’un dominant (A) associéau gris, l’autre récessif (a) associé au blanc ;
– le gène responsable de la texture du pelage est présent sous la forme de deux allèles, l’un dominant (B) associé au lisse, l’autre récessif (b) associéau rude ;
– les gènes responsables de la couleur et la texture du pelage sont sur des chromosomes différents ;
– chaque parent donne, au hasard, à son descendant une copie d’un des deux chromosomes de chaque paire, et ce indépendamment de l’autre parent.
la distribution théorique des cobayes de la génération 2 si le modèle mendélien tient est ![]()
![]()
Or pour une loi ![]() on lit dans la table fournie en annexe
on lit dans la table fournie en annexe ![]()
1.33<7.81 : Ces résultats expérimentaux sont conformes au modèle mendélien au niveau 0.05.
![]() En pratique, il arrive que l’hypothèse ne donne pas la valeur de certains paramètres de la loi.
En pratique, il arrive que l’hypothèse ne donne pas la valeur de certains paramètres de la loi.
On est alors conduit à estimer la valeur de ces paramètres à l’aide des données observées.
On peut montrer qu’alors le théorème ci-dessus reste valable mais la variable
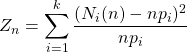 converge en loi vers la loi du
converge en loi vers la loi du ![]() à
à ![]() degrés de liberté.
degrés de liberté.
![]() est le nombre de paramètres à estimer (2 pour une loi normale,1 pour une loi de Poisson ou 0 pour une loi uniforme…)
est le nombre de paramètres à estimer (2 pour une loi normale,1 pour une loi de Poisson ou 0 pour une loi uniforme…)
Exemple 13
Dans une population d’invertébrés marins, la phosphatase acide présente trois allèles ![]() ,
, ![]() et
et ![]() . Les proportions des cinq phénotypes observés sont de 25
. Les proportions des cinq phénotypes observés sont de 25 ![]() , 106
, 106 ![]() , 113
, 113 ![]() , 9
, 9 ![]() et 15
et 15 ![]() .
.
Cette population est-elle à l’équilibre de Hardy Weinberg ?
On commence par calculer les fréquences alléliques : (N=268)
![]()
![]() (premier paramètre à estimer)
(premier paramètre à estimer)
![]()
![]() (deuxième paramètre à estimer)
(deuxième paramètre à estimer)
![]()
Sois ![]() (La population est à l’équilibre)
(La population est à l’équilibre)
Les fréquences respectives des génotypes ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() seront
seront ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]()
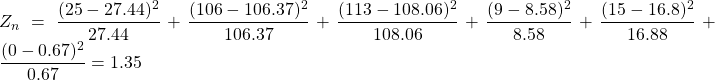
(Exemple de calcul ![]() )
)
Or ici ![]() converge vers une loi du
converge vers une loi du ![]() à
à ![]() degrés de liberté (2 paramètres ont été estimés )
degrés de liberté (2 paramètres ont été estimés )
On lit sur la table ![]() et
et ![]() donc on accepte
donc on accepte ![]()
Exemple 14
a)Une population de Pétrels a été échantillonnée (84 individus ont été capturés) puis caractérisée pour différents marqueurs biochimiques par électrophorèse des protéines. Pour l’un de ces caractères, trois phénotypes [S], [T] et [ST] ont été observés dans des proportions de 35 [S], 18 [T], et 27 [ST] soit un total de 80 individus. Aucun résultat n’a été obtenu pour les quatre individus restants et les expérimentateurs ont considéré qu »il s’agissait d’erreurs de manipulation.
![]()
![]() (premier paramètre à estimer)
(premier paramètre à estimer)
![]()
Sois ![]() (La population est à l’équilibre)
(La population est à l’équilibre)
![]()
Ici ![]() converge vers une loi du
converge vers une loi du ![]() à
à ![]() degré de liberté (1 paramètre a été estimé )
degré de liberté (1 paramètre a été estimé )
On lit sur la table ![]() et
et ![]() donc on rejette
donc on rejette ![]() .
.
b) Ayant un doute sur les résultats, les expérimentateurs reprennent les données en postulant l’existence d’un troisième allèle, nul, appelé ![]() . Le phénotype [O] serait silencieux c’est à dire non détecté par électrophorèse et les phénotypes [SO] = [S] et [TO] = [T].
. Le phénotype [O] serait silencieux c’est à dire non détecté par électrophorèse et les phénotypes [SO] = [S] et [TO] = [T].
![]() ,
, ![]() ,
, ![]() et
et ![]()
![]() donc
donc ![]()
![]() donc
donc ![]()
![]()
![]() , du aux erreurs d’échantillonnage et à la méthode utilisée, une méthode dite de Berstein permet d’obtenir les valeurs corrigées suivantes :
, du aux erreurs d’échantillonnage et à la méthode utilisée, une méthode dite de Berstein permet d’obtenir les valeurs corrigées suivantes :![]() ,
, ![]() et
et ![]()
Sois ![]() (hyphothèse triallélique+ population est à l’équilibre)
(hyphothèse triallélique+ population est à l’équilibre)
![]()
Ici ![]() converge vers une loi du
converge vers une loi du ![]() à
à ![]() degré de liberté (2 paramètres estimés )
degré de liberté (2 paramètres estimés )
On lit sur la table ![]() et
et ![]() donc on accepte
donc on accepte ![]() .
.
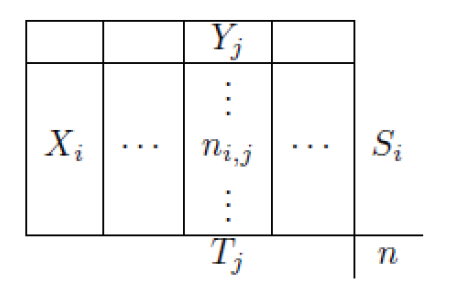
![]() Test d’indépendance ou d’homogénéité
Test d’indépendance ou d’homogénéité
On considère ici un couple ![]() de variables aléatoires,
de variables aléatoires, ![]() à valeurs dans
à valeurs dans ![]() et
et ![]() à valeurs dans
à valeurs dans ![]() .
.
Si ![]() , la loi de
, la loi de ![]() est donnée par une matrice
est donnée par une matrice ![]() . Le problème qui nous intéresse dans ce paragraphe est de tester l’indépendance des variables
. Le problème qui nous intéresse dans ce paragraphe est de tester l’indépendance des variables ![]() et
et ![]() .
.
On calcule les effectifs marginaux : ![]() est la somme des termes sur la i-ème ligne,
est la somme des termes sur la i-ème ligne, ![]() est la somme des termes sur la j-ième colonne.
est la somme des termes sur la j-ième colonne.
On calcule les effectifs théoriques :![]()
Sous l’hypothèse ![]() , on a
, on a ![]()
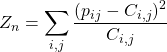 converge en loi vers la loi du
converge en loi vers la loi du ![]() à
à ![]() degrés de liberté.
degrés de liberté.
En effet Le nombre de paramètres estimés est ![]() puisque la donnée des
puisque la donnée des ![]() premiers coefficients de la loi de
premiers coefficients de la loi de ![]() donne le dernier (et idem pour
donne le dernier (et idem pour ![]() ).
).
Exemple 15
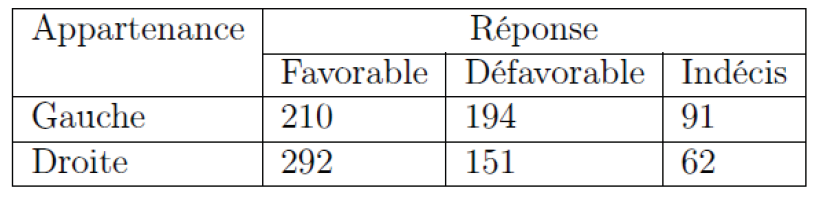
Un échantillon de 1000 personnes ont été interrogées sur leur opinion à propos d’une question qui sera posée à un référendum. On a demandé à ces personnes de préciser leur appartenance politique. Les résultats sont donnés par le tableau suivant:
On veut savoir la réponse au référendum est indépendante de l’opinion politique.
ici ![]() ,
, ![]() ,
, ![]() .
. ![]() ,
, ![]() .
.
Donc ![]() ,
, ![]() …..
…..
![]()
et ![]() converge en loi vers la loi du
converge en loi vers la loi du ![]() à
à ![]() degrés de liberté.
degrés de liberté.
On lit sur la table ![]() et
et ![]() donc on rejette
donc on rejette ![]() .
.
Les tests du ![]() permettent aussi de tester l’homogénéité de plusieurs échantillons.
permettent aussi de tester l’homogénéité de plusieurs échantillons.
La mise en place pratique du test est la même que pour le test d’indépendance.